Musical Tuning and Temperament
The following theoretical excursion outlines the theory behind all musical tuning system, temparement, and provides a profound discussion of the theory behind the Hermode Tuning algorithm.
History of Tuning Systems
Whoever speaks about the tradition of musical tuning in western culture refers to the Pythagoreans who have invented about 2,500 years ago a musical system basing in a sequence of fifths being tuned to just intonation. But they haven't been the first with this idea. Already the oldest ever discovered musical instrument, a 35,000 years old flute, shows some fifths being tuned near to just intonation. Even the Chinese music culture was basing in a system of fifths in just intonation, long before the Pythagoreans redeveloped it. The most important objection against the equation of the Pythagorean tuning model with the ideals of actual western music is however: The Pythagorean tuning model doesn't consider the thirds as autonomous intervals. Understand the Pythagorean tuning model with the help of the following figure:
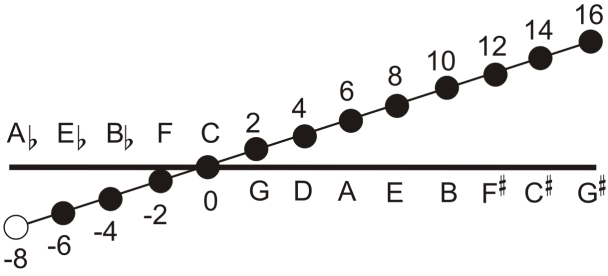This figure contains a horizontal line, illustrating the level of the common
equal temperament. The halftones of equal temperament are tuned to an equal distance of 100 Cents,
consequentially its fifths are tuned to 700 Cents. But the two tones of a fifth in just intonation
should be tuned to a frequency ratio of 2 : 3 and this corresponds to a value of 702 Cents. Therefore,
when positioning the C on the level of equal temperament, the following fifths will drift upwards, the
preceding will drift downwards, shown by their added Cents values. This tuning model, basing on the
twelve fifths intervals from E-flat on up to G-sharp is not closed, the fifth G-sharp/E-flat is unplayable as A-flat,
shown in white, doesn't exist. But this was without relevance as the western music until the early mediaeval
didn't need these tones. By the way: The pitch difference of 24 Cents between the A-flat and the G-sharp of this
tuning system is named the Pythagorean Comma.
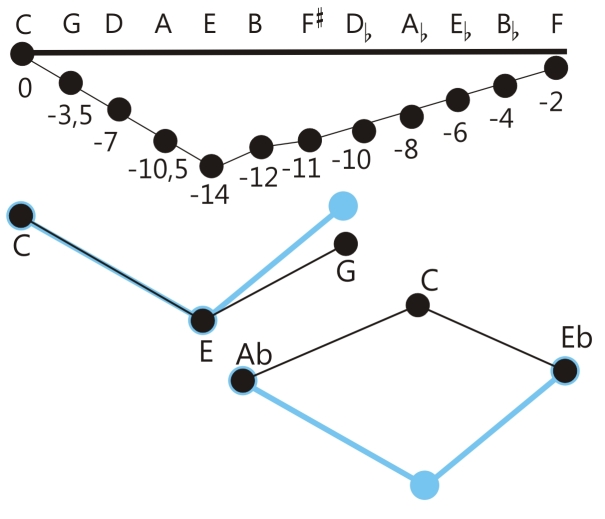
The Pythagorean tuning system was mandatory for the western music until the end of the 13th century. Thirds haven't been regarded as autonomous intervals, they sounded and sound dissonant with this tuning model. However in the 14th century some musicians - it is supposed that they were English singers - experimented with the major third and embedded it between the two tones of the fifth so that a consonant chord was arising. A major chord according to our modern definition. See the following figure of the example of a C-major chord:
The black colored major third E in just intonation has a much lower
position than the red colored of the Pythagorean tuning model. The difference of both positions is 22 Cents,
the so-called Syntonic Comma. If ever you will come across the musical term "Comma" without additional
designation, this Syntonic Comma will be meant and not the Pythagorean one.
Just intonation means a frequency ratio of 2 : 3 for the fifths and of 4 : 5 for the major thirds. The values of other intervals e.g. of the minor thirds are derived from these basic values. The reason for the clearer and stronger sound of chords being tuned to just intonation is based on a better synchronicity of the partial tones of the concerning notes and a better synchronicity of their difference tones. Difference tones occur as soon as at least two different tones are sounding simultaneously. We will explain this with the examples of an A-major chord and an a-minor chord. Both tuned on the one hand to just intonation and alternately to equal temperament.
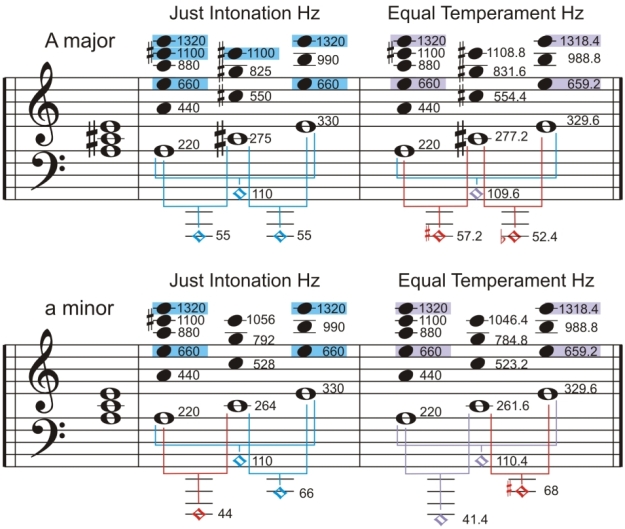Understand this figure as follows: The upper half shows an A major chord
with some of its partial tones and its resulting difference tones. The original tones are displayed as whole
notes, the partial tones as black dots, the difference tones are shown as square notes. The left bar of each
system shows the frequencies on the basis of just intonation, the right bar shows the frequencies of equal
temperament. The lower half shows an a minor chord with the same tuning variants. The frequencies of concordant
partial tones show a blue background, others with very little deviations show a violet background.
The difference tones are colored blue when in perfect tune, violet means little differences to perfection
and red means a big deviation.
The major chord in just intonation shows a high accordance of all tones. Against this its equal tempered counterpart shows two difference tones tones A-flat and A-sharp sounding in conflict with the original A. The a minor chord produces already in just intonation a difference tone G being not in concordance with the original tones. But also its equal tempered counterpart shows only one problematic difference tone, namely a C-sharp. The other difference tones show only few deviations to perfection.
With other words: In just intonation a major chord sounds better than a minor chord. In equal temperament a minor chord sounds better than a major chord. It is for this reason that keyboarders actually prefer minor chords when performing sound plains. But musically considered it is a wrong world.
Back to the 14th century: The singers and the musicians with wind and string instruments had no big problem when performing music in just intonation. OK, they had to use their ears for controlling the pitch, but this was more or less an individual problem and not a fundamental one. But for keyboards with their fixed tuning models this new aesthetic meant an unpleasant revolution. Things already start to become difficult when trying to tune one single key e.g. C-major to just intonation. See the figure below:
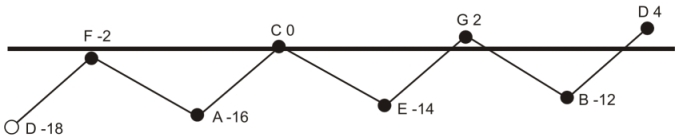The vain attempt to tune all triads of C-major to just intonation.
The major chords F-A-C, C-E-G, G-B-D as well as the minor chords A-C-E and E-G-B are tuned to just intonation.
But the chord D-F-A would require a low D, tuned 22 Cents lower than in the G-B-D chord. You remember the
Syntonic Comma? It has struck again.
Nevertheless some actual keyboards present such tuning tables named for instance 'just C-major'. But now you know: These tables are nonsense!
Therefore it was tried to solve this problem by other means. A tuning table with a sequence of major thirds tuned to just intonation has been developed. See the figure below:
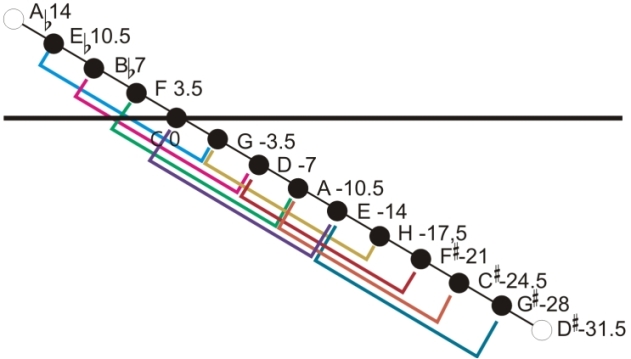This is the so-called Meantone 1/4 Comma tuning model. The fifth line
now moves downwards, so that eight major thirds, beginning with E-flat - G and ending with E - G-sharp, are tuned to just
intonation. Some ancient keyboards were additionally equipped with an A-flat and a D-sharp key so that their octaves
comprised fourteen instead of twelve tones. As a result of the better tuned thirds, the fifths are tuned by
1/4 of the Syntonic Comma narrower than in just intonation. Therefore they beat faster than with equal temperament,
nevertheless a complete major chord sounds with this tuning model much better than with Pythagorean tuning or
with Equal Temperament.
The C major chord shown by the 1/4 Comma Meantone tuning model illustrates
its tuning improvement. The major third C - E is perfect in tune, only the fifth G shows a little deviation from
its ideal position, shown in blue.
Alternately less extreme tuning models have been designed, e.g. Meantone 1/5 Comma. Imagine the Meantone 1/4 Comma tuning line turned a little counterclockwise so that the major thirds will be a little less perfect and the fifths nearer to their ideal position, see the drawing below.
The C major chord with the 1/5 Comma Meantone tuning model. The
effective tuning is shown in black, the ideal tuning values are shown in blue.
Meantone tuning models have been used mainly until the 17th century, but even some actual existing pipe organs still contain such tuning models. These organs are praised for their warm sound, and many organ players prefer them. Prefer them in spite of their musical limitations.
Musical limitations? Indeed, with this tuning model and 12 tones per Octave it is only possible to perform music between E-flat major and A-major and their corresponding minor parallels. With 14 tones per octave the possibilities will be a little widened, nevertheless the system would not be closed. For the music between the 14th and 17th century this was of less importance. But from about the 18th century on there came up calls for a closed tuning system. The result was not immediately the Equal Temperament as it was desired to tune at least the keys in the middle of the fifth circle, e.g. F-major, C-major and G-major better than the rarely used keys with many accidentals. The following figure shows such a typical Well-Tempered tuning model, named Kirnberger III:
This Kirnberger III tuning model shows a meantone fifth sequence from C to E,
subsequently the fifths line E to F moves upwards in more or less Pythagorean steps. Now the system was closed.
It is common to name such tuning models "temperaments". The result are different tuned chords, here shown by the
examples of a C-major and an A-flat major triad. C-major sounds rich as its frequencies are positioned near to the
perfect tuning ratios, shown in blue. A flat major against this sounds quite horribly. But these chords now could
be performed and the inventors of this tuning method praised this system as Well Tempered.
Imposing a problematic object with a euphonious name is no invention of modern times.
Through the 18th and 19th century it became more and more desired to tune the chords of the keys with many accidentals to better frequency ratios. Therefore more flattened temperaments have been developed with the inevitable result that the previously better tuned chords got an inferior quality.
Three unequal temperaments: Kirnberger III colored green, Valotti colored red
and Prelleur colored blue, the latter two more and more approaching the horizontal line of Equal Temperament,
shown by black colored dots.
Status Quo
Meanwhile we have almost lost sight of the qualified musicians as members of string and wind ensembles and as singers of well-trained choirs. We repeat: They control the pitch of the performed notes dynamically according to their function in the harmonic environment. Making music together with a keyboard is for them almost a plague. Pianos with their rapidly fading tones disturb less, but pipe organs with their sustained tones cause intense conflicts. Many choir leaders complain about this problem. Besides, all simulations of orchestral music by virtual instruments sound poor when performed with fixed tuning models.
Hermode Tuning
That's why Hermode Tuning has been developed. It imitates the tuning behavior of the musicians mentioned above. The fundamental idea is simple: All Note-On and Note-Off messages are continuously analyzed and the actual ringing notes will be tuned mutually as near as possible to the frequency ratios of just intonation. However this becomes difficult as soon as one has to control the tones in real time by inaudible retuning steps and with a tight approach to the level of the default equal temperament. But these difficulties have been overcome, and when opening the Hermode Tuning window you will get an insight in its tuning process
Hermode Tuning is integrated in most of our iOS audio apps, and it is also part of the function set of Apple Logic and Cubase. Meanwhile even the first acoustic pipe organ with Hermode Tuning has been developed as well.
You can find more information and musical examples at the hermode.com website.